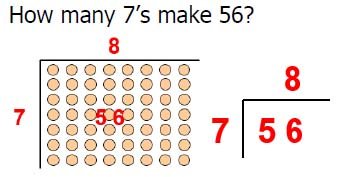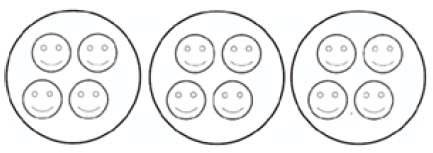
Children are encouraged to develop a mental picture of the number system in their heads to use for calculation. They learn to count in different steps and experience sharing and grouping using a variety of practical resources and real life objects. They develop ways of recording calculations using pictures, etc.

It is important to note that ‘sharing’ is an experience of division only if it is ‘sharing equally between’.

Use of language and visual representation is important – remember the visual image for sharing will be different for grouping. Create topic links where possible.

e.g 6 ÷ 2 ...

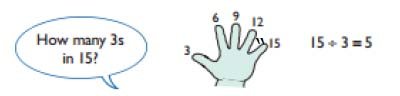
Grouping – “How many 2’s in 6”

How many 5’s in 15?

Division situations of this kind have what is called the inverse of multiplication structure.

Setting the problems in both real life/topic context and solving them with concrete apparatus will support children’s understanding.

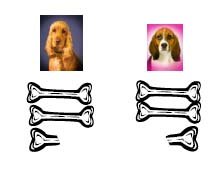“I have got 5 bones to share equally between my two dogs. How many bones will they get each?”

It is important that children have lots of experiences in grouping and sharing for division using practical apparatus, arrays and pictorial representations in the early stages of understanding this concept.

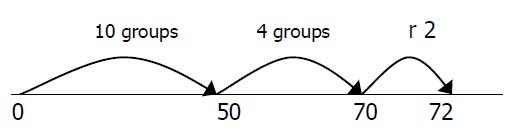
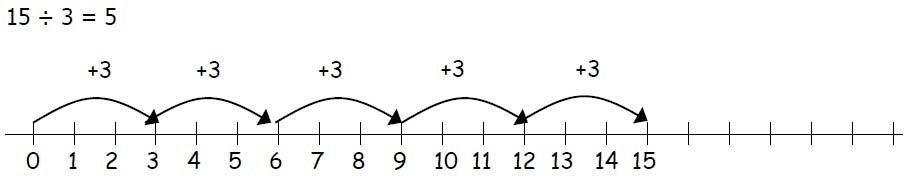
Grouping can be shown easily on a number line.
Group from zero in jumps of the divisor to find ‘how many groups of 3 are there in 15?’

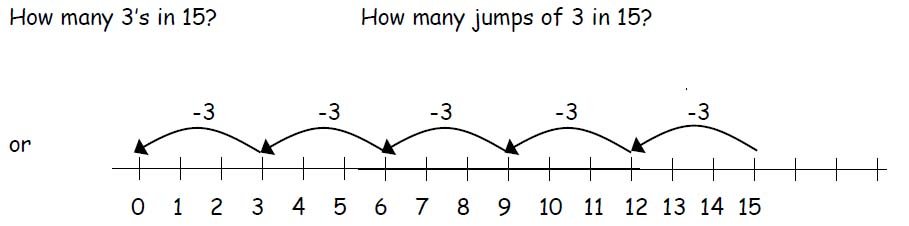
It is important that children have experience of division on a number line in both ways, for connections to be made.

Use of Cuisenaire and Number tracks support the concept of grouping on the number line.

Most children should be able to use an empty number line for division by Year 3. These recordings help to support mental strategies.

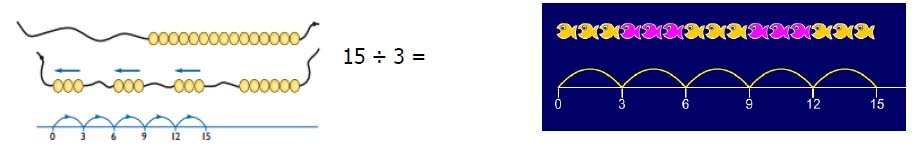
Children will continue to use repeated addition and subtraction but will progress onto using a blank number line:

Grouping

How many 4’s are in 24?

Becoming more efficient using a numberline:

Children need to be able to partition the dividend in different ways.

Children should also move onto calculations involving remainders.

A car holds 4 people. How many cars are needed to transport 49 people? (group and round up)

Moving onto:

It is important that children continue to explore division as sharing and grouping, and to represent calculations on a numberline until they have a secure understanding.

The use of the bar model is another useful way of demonstrating division in a visual way.

How many groups of 2 in 18?

In Year 4, children will begin to learn the short division representation with the use of place value resources. Alongside pictorial representations and the use of models and images, children should progress onto short division using a bus stop method.

Place value counters can be used to support children apply their knowledge of grouping. Reference should be made to the value of each digit in the dividend.

Cuisenaire rods can also be used to reinforce this concept.

Short division of a two-digit number can be introduced to children who are confident with multiplication and division facts and with subtracting multiples of 10 mentally, and whose understanding of partitioning and place value is sound.

When children have conceptual understanding and fluency using the bus stop method without remainders, they can then progress onto ‘carrying’ their remainder across to the next digit.
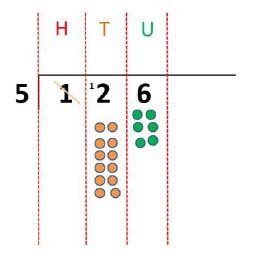
Place value counters can be used to support children apply their knowledge of grouping. (Dienes could also be used but place value counters are more efficient.)

Each digit as a multiple of the divisor
‘How many groups of 3 are there in the hundreds column?’
‘How many groups of 3 are there in the tens column?’
‘How many groups of 3 are there in the units/ones column?’

Formal Written Methods
Formal short division should only be introduced once children have a good understanding of division, its links with multiplication and the idea of ‘chunking up’ to find a target number (see use of number lines).

Short division to be modelled for understanding using place value counters as shown below. Calculations with 2 and 3-digit dividends.

Continued as shown, leading to the efficient use of a formal method. The language of grouping to be used
E.g. 1435 ÷ 6

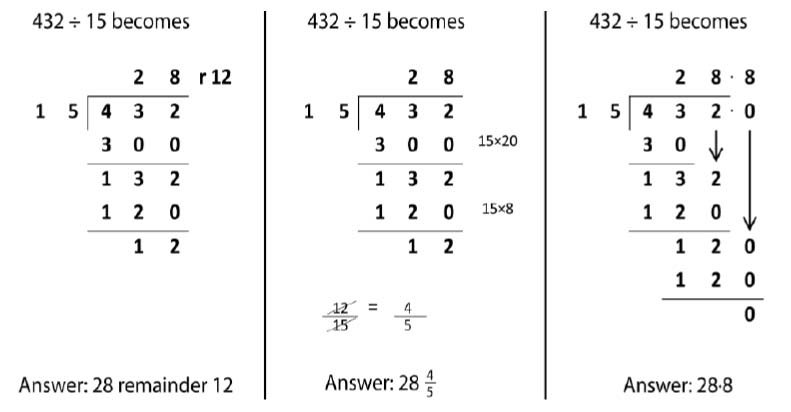
Children begin to practically develop their understanding of how to express the remainder as a decimal or a fraction.
Ensure practical understanding allows children to work through this (e.g. what could I do with this remaining 1? How could I share this between 6 as well?)

Please click on the link below to watch a video modelling the short division with no remainders strategy.

 Short division with no remainders

By the end of Year 5, most children will be confident to use short division. Children will continue to explore division as sharing and grouping, and to represent calculations on a number line as appropriate. In Year 6, the formal long division method is taught using numbers up to ThHTU ÷ TU.

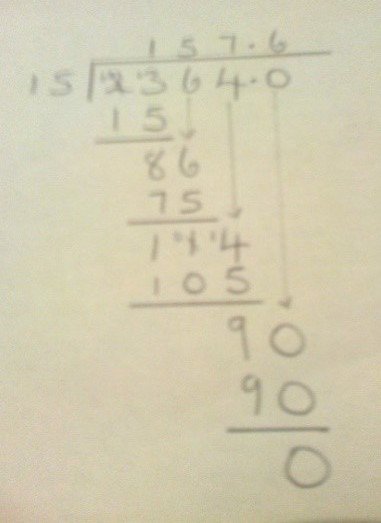Quotients should be expressed as decimals and fractions

E.g. 2364 ÷ 15

At year 6, the remainder should be expressed as a fraction or decimal.

The following are examples of long division from the National Curriculum

Please click on the link below to watch a video modelling long division with a decimal answer

Long division with decimal answer